Decomposing numbers in kindergarten

Common Core standard K.OA.3 states, ``Decompose numbers less than or equal to 10 into pairs in more than one way, e.g., by using objects or drawings, and record each decomposition by a drawing or equation (e.g., 5 = 2 + 3 and 5 = 4 + 1).''

Although it falls under the general heading of addition and subtraction, the mathematical concept that this exercise is supposed to teach kindergartners is mystifying.  By ``pairs'', does it really mean ``groups''?  Is it an introduction to odd and even numbers?  The commutative property?  Transitivity?  Algebra?  Combinatorics?  Or to impress on the kindergartner that both 4 + 1 and 2 + 3 equal 5?

We don't think it will achieve the last objective, if that is the intent.  Let's say a problem begins with 5 apples and asks a kindergartner to place them into two bowls in various ways (see footnote below).  As the problem proceeds, no matter how they are separated, a kindergartner will likely only perceive all 5 apples as one group.

[As we try to put ourselves into a kindergartner's mind, we'd be thinking (but writing with an adult mind's language), ``M. Cézanne, why would you want me to separate 5 apples into two groups?  That's nonsensical.  I just count 5 apples.  Apples are all the same; they belong together.'']

Separating apples into arbitrary groups is an abstraction; any intelligent kindergartner will want to put the apples back together.  Kindergartners are at an age of concrete thinking, where they are learning to recognize common and distinct characteristics, so a common exercise is to groups things together that share a characteristic, not separate them.

You can force them to draw pictures of the separate groups and record numbers and equations, but the intent of the problem will be lost.  No kindergartner will be impressed that there are myriad ways to separate the apples, because no matter how the apples are separated, the total remains the same.  If you try to impress on a kindergartner the mathematical abstraction that both 2 + 3 is 5 and 4 + 1 is 5, and isn't that fascinating, they'll say ``duh'', because they saw 5 apples all along.  And their instincts would be correct; it's not a mathematically important result that 23 + 19 and 11 + 31 both add to 42.

What then, is the pedagogical theory behind assigning such a task to a kindergartner?  We think there is none.  A problem shouldn't be posed just because it can be, especially at such a young age; the purpose of the question needs be clear.

Addition concepts are neither taught nor reinforced by decomposition; addition concepts are introduced by putting two groups together and counting the total.  The way we've been teaching addition all these years still works.

CCSSI's example (Table 1 in the Standards), to figure out all possible ways to distribute five flowers among grandma's two vases is particularly unsettling, and worse than the apple problem we used.  This is a blog about mathematics, not gender issues, so we shouldn't be raising the point that the question is sexist, but there, we said it anyway.  More importantly, though, the flower question is pretty far removed from a kindergartner's experiences, and at that age, coalescing a child's amorphous experiences by way of a well formulated question is a parallel task of the educator and of the curriculum, and math questions should reflect this dual purpose.  What makes the flower problem particularly shallow is that it creates no open paths for forward learning past the obvious answers to the question.  There are a bunch of possibilities, list them all or draw them all, and that's it; the problem is finished.

A well-conceived question will be remembered, not for the answer, but for the quandaries it poses.  Many math questions are solved and then quickly forgotten because they lack this dimensionality.  Simply put, the questions are dull.  Math textbooks and workbooks are filled with dull, pointless questions.

***

K.CC.6 states ``Identify whether the number of objects in one group is greater than, less than, or equal to the number of objects in another group, e.g., by using matching and counting strategies.''

Certainly within the realm of a kindergartner's experience are the ideas of equal, less and more.  A child is more likely to complain that his brother got more cookies than he than to thank his parents that the cookies were distributed equally.  Certainly along with counting, that two quantities are equal is a critically important concept, followed in developmental sequence by one quantity is more or less than another.

Counting, equality and comparison should comprise the Big Three of Kindergarten and you can go plenty deep with these three concepts before moving on to addition and subtraction in Grade 1.

K.CC.6, unfortunately, suggests activities to evolve these concepts that would bore a lawyer.  If we take K.OA.3 and K.CC.6 and consider them together, then rather than posing a decomposition question that compares the results with the original number (the flower question), we would devise a decomposition question that compares the resulting numbers with each other.

We suggest an exercise for decomposing numbers that has an element of stealth: Ask a kindergartner to share a basket of (10 or less) apples with a classmate, but do not tell them how.

Will they give just one apple to the classmate?  Will they try to share equally?  If they share just one apple, you can egg them on with the question, ``Is that fair?''  What will happen if they try to, but realize they cannot share equally?  (Repose the question with different numbers of apples.)  There doesn't have to be a single correct answer, and they can work out this problem in myriad ways (counting by 1's, 2's, estimating, making piles, etc.)  Not only does it reinforce the concept of sharing (cross discipline!), they're discovering the concepts of equality, odd and even, division, remainders, greater than and less than, and maybe even fractions long before those abstract terms are formally introduced.  It is well within a kindergartner's capabilities to count apples and grapple with the possibility of sometimes having an apple left over, and wondering what that means, even if not every kindergartner fully ``gets it''.  But for those students with insight, it opens the possibility of ``teachable moments'', when that one student suggests cutting an apple in half.  You can't cut a flower in half and place it in a vase (right, Mr. van Gogh?).

When you're sharing apples, it makes sense to separate the apples into two groups, mine and yours.  By not being an answer-oriented question, but rather an exploration of numbers question, there's a lot more to be learned and remembered.

As it seems will become a familiar theme in this blog, learning concepts should precede (even by years) abstractions.

Footnote:
Who's going to do the separating in K.OA.3?  Our guess is the teacher, who, following a CCSSI-based textbook lesson plan, gets a non-response after asking a group of kindergartners, ``How many ways can you separate these apples into 2 groups?''  (CCSSI, Table 1, suggests using two vases and some flowers.  Why would you leave a vase empty?)  The students won't know what to do, and the teacher will have to demonstrate.  Useless.

************

ADDENDUM FOR KINDERGARTEN TEACHERS
January 2013

We have been getting hundreds of visits directly to this particular blog post resulting from online searches on the terms ``kindergarten decomposing numbers’’ and the like.

The most pathetic variation on this search is the one that asks for ``kindergarten decomposing numbers worksheets’’.  We cannot imagine any educational experience more tedious and spirit-killing than giving worksheets to kindergartners, but we understand that teachers are essentially enslaved to Common Core’s standards, of which K.OA.3 stands out in its inappropriateness.

We are going to suggest two related activities in lieu of Common Core’s suggested exercises that will allow students to (1) practice counting and (2) learn about what a number is really comprised of, and simultaneously will allow teachers to observe and gauge students’ becoming proficient at both.

The first activity is a commonly available game called Chutes and Ladders.  We think this game offers an excellent exercise in counting.  Time could be set aside every week for everyone to play, in groups of four to a board.  The rules are easy, but what teachers should be looking for is how students count.  Students will progress differently and that is what teachers want to be on the lookout for.  Weaker students will count one at a time.  Stronger students will start to group numbers.


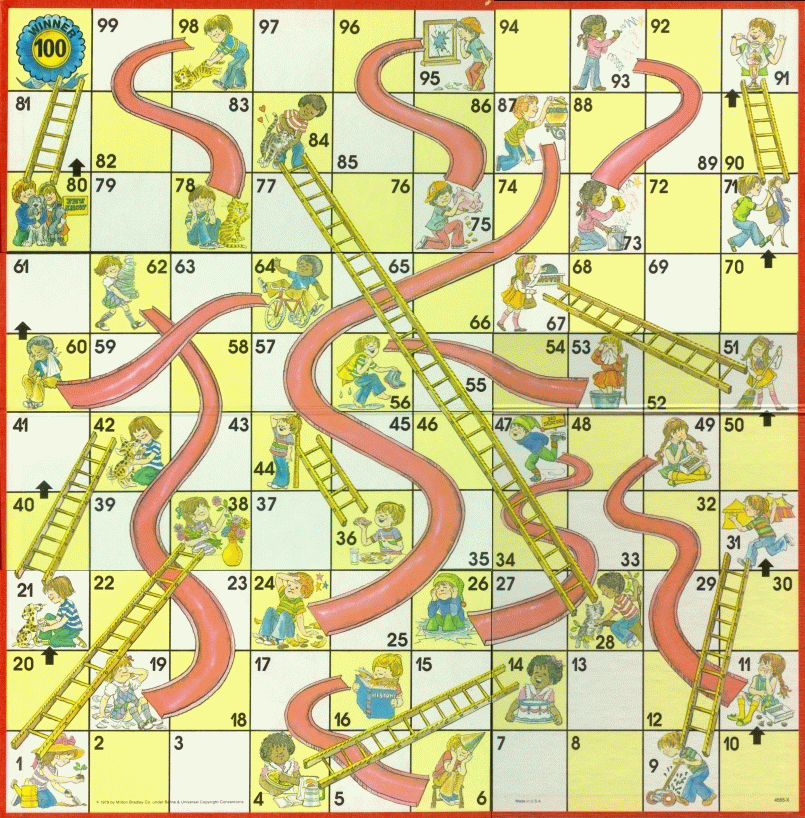
For instance, if a student’s piece is on space 27 and they spin a 6 (ignoring addition for the time being), the students who readily pick up the ability to jump right 3, then up 1, then left 2 (perhaps saying something like ``three-four-six’’) to space 33 (instead of counting one at a time) are students you can check off in your gradebook as unlikely to ever need basic math help.  Counting in groups like that is an indication of real math understanding, analogous to a proficient reader who reads in phrases, not one word at a time.  A student’s ability to group certainly encompasses Common Core’s silly ``decompose numbers’’ standard and you can assuredly consider the standard attained.

Just as students make individual breakthroughs in learning to read and the like, so too will you witness breakthroughs in counting.  As students make the leap to grouping numbers, leave them be.  As you rotate around the room, focus instead on the students still counting one at a time and suggest/encourage/demonstrate grouping as necessary.  No need to push it; grouping—an early indicator of number sense—will (hopefully) come.

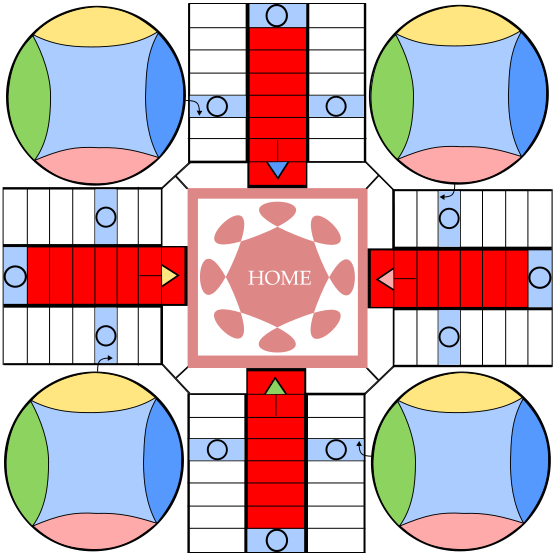
Later in the year, it’s time to graduate to the next counting board game, Parcheesi.  The complete rules are complicated, but students can play a simplified version.  Parcheesi uses 2 six-sided dice (addition optional) and as the pieces move around the board, the movements can also be broken into sections: down, around, and up the spaces.  Again, students who continue to count spaces individually will need the most help.  Students who quickly figure out how to count by twos or threes, or jump multiple spaces while mentally keeping track of the total can be left alone.


If you try these techniques, please let us know how it works out.