The National Assessment of Educational Progress (``The Nation’s Report Card’’) in 2007 posed the following question:
Sidestepping for now the issue that only half of eighth graders correctly solved an elementary school problem, calculator allowed, the intrigue lies in the distribution of wrong answers:
40% chose fairly equally between answers B and E, but only 10% chose C or D, raising the inference that incorrect choices were not random, but reflected the result of a process.
Although the fractions in B and E are in the exact opposite order, the choices share a characteristic: B has both the numerators and denominators in increasing order left to right; in E, both decrease. Either of these answers, but neither C nor D, would result from the misapplication of commonly taught shortcuts in which students compare numerators or denominators instead of fractions in their entirety. We state the obvious for the record, but any version of these ``tricks’’ only applies when either the numerator or denominator remains constant. Nevertheless, it is apparent that a significant proportion of students resorted to such shortcuts in a situation where they do not apply.
***
Effective K-12 mathematics education reform requires deliberate steps: the identification and addressing of specific difficulties, among which fractions’ myriad aspects perennially remain near the top of the list.
There are many hurdles to learning fractions well, but one of the first is semantic: the introduction into the lexicon of two of the most commonly misidentified words in K-12 mathematics education, numerator and denominator. Concurrent with many students’ confusing these two Latin-derived, similar sounding words is the often overlooked historical fact that fraction notation is arbitrary.
While much research has been done on reading dyslexia, we’d venture little has been done for ``math dyslexia’’, i.e., students who mix up the numerator and denominator. Simpler vocabulary, like ``top’’ and ``bottom’’, may help, but we make note of one inherent advantage for students learning mathematics in other languages, such as Chinese, in which the word for numerator is 子, meaning ``child’’, and the word for denominator is 母, meaning ``mother’’, which seem far easier to differentiate.
***
Rather than confronting a systemic weakness exposed by the NAEP, regardless of whether the root cause is in the language, in fraction notation, or from students’ failure to differentiate, Common Core makes its initial foray into the topic of comparing fractions with 3.NF.3d:
``Compare two fractions with the same numerator or the same denominator by reasoning about their size...and justify the conclusions, e.g., by using a visual fraction model.’’
Instead of highlighting and clarifying for the sake of students two conceptually different models, Common Core merges the two. In presentation and practice, the difference between the two situations is stark: one of the concepts is straightforward; the other significantly more abstract, but that distinction is likely to be obfuscated by this standard.
The latter scenario (we’ll call it Different Numerator Common Denominator, or DNCD), is the simpler of the two, and rarely misunderstood. This is a direct comparison and should be introduced early on, immediately following learning how to name, identify and represent fractions. That’s because fractions with a common denominator can be compared by counting, a previously learned concept:
Which fraction is greater?
Students are already familiar with comparing whole numbers; this represents an incremental increase in complexity.
Fractions are compared first by counting sections, resulting in students’ conceptual understanding that a visual size comparison and the numerator number count coincide.
It then follows logically that students should learn to add and subtract fractions with common denominators (with the important understanding that the numerators add, but denominators don’t).
22% of fourth graders taking the 2005 NAEP chose answer C in the following question, which means there’s a lot of work to do in classrooms, even in the most basic fraction arithmetic:
This sequence of basic fraction skills—name, identify and represent fractions, and compare/add/subtract fractions with common denominators—would make a reasonable set of goals for Grade 3.
***
3.NF.3d’s former scenario (we’ll call it Common Numerator Different Denominator, or CNDD)—comparing fractions with common numerators but different denominators—raises a variety of issues.
The first is that this scenario is artificial: encountering two fractions that share the same numerator is either a coincidence, or worse, a contrived problem; it is never in the standard repertoire for students to manipulate fractions to obtain a common numerator (but see this challenging elementary school problem).
In contrast, seeking common denominators is the Holy Grail of fraction arithmetic.
So how will CNDD manifest itself in the classroom?
Consider this activity: The teacher hands students the strips pictured below and asks students to shade in ½ of the first strip and ⅓ of the second strip.
Teacher: Which is greater?
Student: ½
Teacher: Now in this next problem, shade in ¾ of the first strip and ⅗ of the second trip: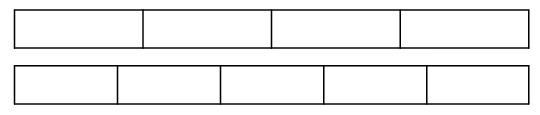
Student: Ok, I did it.
Teacher: Which is greater?
Student: ¾
Teacher: Look at both problems. You remember that when comparing fractions with the same denominator, as the numerator gets bigger, the fraction gets bigger, but now we see that if the numerators are the same, as the denominator gets bigger, the fraction gets smaller, and isn’t that fascinating, children?
Maybe Grade 3 students learning fractions for the first time will understand the numerical distinction; maybe not.
More importantly, does the concept really need to be taught in the classroom that if you cut something into more pieces, the pieces are going to be smaller? We here at ccssimath.blogspot.com think this particular concept should be left out of formal education. This is a concept that every student can and will discover on their own. Likely, students younger than Grade 3 already know this intuitively.
Formalizing this concept with numbers will likely add confusion, not lead to clarity. That’s because the CNDD comparison of fractions doesn’t involve a simple tally. However, counting is easier and many students will resort to what they know. There is counting in the sense of a pie cut into 10 equal sections will have ten pieces and a pie cut into 8 equal sections has eight pieces, but the size comparison is inverted: more pieces means a smaller size for each piece.
Thus, if presented out of context, or without a diagram, many students with conceptual weakness will compare ⅔ and ⅖ and, with a simple count, conclude ⅖ is greater.
Under this analysis, 3.NF.3d’s weakness becomes apparent: when the numerical comparison of fractions with ``same numerator'' and ``same denominator'' are lumped into the same standard, there is the very real likelihood that students will conflate the two.
It remains a topic for another blog post, but we should note that students’ gaining an understanding that fractions with different denominators can be worked with numerically in one problem is a tremendous leap in abstraction—it makes sense to wait until Grade 4, after fractions have had a year to sink in—but even then the order of presentation of uncommon denominator concepts should be considered carefully. Common Core has not considered any of these issues. Instead, it bounces around in both Grades 3 and 4 between common and “uncommon” denominator concepts without a logical progression. That is something that the savviest elementary educators cannot easily compensate for; there are those darned tests.
(Even wackier, Common Core in Grade 3 describes whole numbers as fractions with denominator 1, which is completely out of place and unnecessary until fraction multiplication is introduced in Grade 5.)
***
In our analysis of 3.NF.3d, there is a further distinction between 3.NF.3d’s commingled concepts that is absent from “reason...about their size...and justify the conclusions”, which justifies parsing it. A simple illustration is that, for DNCD, the arithmetical difference between ⅖ and ⅗ is the same as between ⅗ and ⅘ because 3–2=4–3, but for CNDD the difference between ½ and ⅓ is not the same as between ⅓ and ¼.
One thing we know for sure: the analyses of the differences between ½ and ⅓ and between ⅓ and ¼ is not Grade 3 material, and in our opinion, the half teaching of a concept is worse than none. This missing aspect of 3.NF.3d’s expectation is that when comparing fractions’ sizes, there’s more to the reasoning than just which is greater and which is less, but how much greater or less. In other words, how do you determine and compare the value of fractions?
Let’s look again at the Standards. In both Grades 3 and 4 and continuing past Grade 5 into Grade 6, Common Core repeatedly would have students analyze fractions with the use of a ``visual fraction model”, defined in the glossary as “a tape diagram, number line diagram, or area model.” See 3.NF.3b, 3.NF.3d, 4.NF.1, 4.NF.2, 4.NF.3b, 4.NF.3d, 4.NF.4a, 4.NF.4b, 4.NF.4c, 5.NF.2, 5.NF.3, 5.NF.4a, 5.NF.6, 5.NF.7a, 5.NF.7b, 5.NF.7c, and 6.NS.1.
The most advanced ``visual fraction model’’ would be the area model, in which students will arrive at a final answer either by counting the squares or comparing sizes.
Size is important, as they say, but fraction size should be a mere introduction to the more important concept of a fraction’s value. While size is a visual concept, value is the critical mathematical concept.
At a certain point, students need to move past manipulatives.
At a certain point, students need to understand the mathematics.
But nowhere in Common Core does it make this transition. 3.NF.3d’s CNDD compares fractions by showing they have different sizes, but the concept of value is left in this fledgling state for three more years.
This is a shocking oversight. Why is this omission a problem? An illustration of why the concept of value needs to be squarely addressed appears in the 2009 4th Grade NAEP, which gave the following question:
Nationally, 25% of students got the right answer, no better than guessing.
By 8th grade, you’d expect a greater understanding of fraction value:
This question incorporates several concepts, including comparing fractions with simultaneously changing numerators and denominators. While it isn’t absolutely necessary for solving this problem, it might be useful for a student to recognize that the sequence of fractions increases in value. In that manner, a student might know to reject terms like 94/95, 95/96 (B), 99/100, 100/101 (A), all of which occur in the sequence, but that have values greater than 0.95.
As it stands, only 27% of eighth graders on the 2003 NAEP could identify the correct answer, D. More telling was that a greater proportion of students, 34%, chose answer B, recognizing that in this simple pattern, the 95th term will be 95/96, but erroneously reasoning that a fraction with 95 in the numerator would be equal to 0.95. This disconnect shows that a significant number of students lack an understanding of how to determine that fraction’s value.
More students rejected the correct answer, 19/20 = 0.95, and chose a wrong answer, 95/96 = 0.95 because the digits 9 and 5 together coincide visually. This overreliance on visual cues shocks our conscience and shows again that drastic measures must be implemented to wean students from pictures (including visual apps and games) and improve students’ mathematical ability (with paper and pencil) to determine and understand a fraction’s value.
The NAEP question we began with can be analyzed from this point of view as well: students are honing in on numerators and denominators separately and out of context, and not considering the entire fraction as a number unto itself.
This misdirection of students’ focus was the impetus for our choice of title: fractions are numbers, too.
Common Core offers an unprecedented opportunity to offer a clear vision, but in an ill-conceived attempt to be expeditious, calls on Grade 3 students to recognize and describe, without reconciling, two loosely-related mathematical patterns. Those patterns, at different points in their development, will leave students without a full understanding of the nature of fractions, but will nonetheless be drilled, quizzed, and tested. Under the pressure of assessments, it will undoubtedly lead to the introduction, resorting to and misuse of the shortcuts described above.
Students won’t be learning to factor and find LCD’s for at least a year, but by then, the bad habits may be too ingrained to break.
Our recommendation: A better alternative to 3.NF.3d (and the rest of the Grade 3 and 4 fractions standards) would be that fractions with different denominators form an entirely separate unit, starting in Grade 4. (We’ve already laid out what the Grade 3 progression should look like.) Then discussion of the differences in fraction value aligns with how to make such comparisons, and how to find the actual sums and differences of any fractions, all topics that fit in with finding a common denominator, a central, but more advanced topic.
Common Core, if implemented as currently written, will fail to make inroads into fraction numeracy. Indeed, Common Core will ensure that every student in the country will be heading down the same muddled (and puddled) path.
To be continued…
Test yourself on ordering fractions
To be continued…
Test yourself on ordering fractions
Perhaps you have explained this elsewhere, but what were the qualifications of the people who came up with the CC math standards? One would imagine for an important job like that at least 2 qualifications would be needed: a degree or two in math (not math education) and many years of experience teaching math in classrooms (not just any grade, but the grades that match the standards that particular writer worked on). The more I examine the standards, the more it seems that the writers had no idea how children think and learn, and no understanding of how math topics relate to each other. I get the impression the writers were people with weak math skills who did not work directly with children ... possibly that group of people known as Math Educators who lack both real math training (meaning classes like algebra 2, calculus, abstract algebra, etc) and/or classroom experience? Could you please address this question because it might explain a lot.
ReplyDeleteHere is a well-documented article about who was on the CC math work groups....http://deutsch29.wordpress.com/2014/04/23/those-24-common-core-2009-work-group-members/comment-page-1/#comment-9743...A couple of college level mathematicians, a few high school teachers long out of the classroom, NO one with ANY elementary teaching experience, NO one with ANY specialty in early elementary "math education" (a much needed component to the writing of standards for elementary students, I would say) or even middle school math teachers or math educators, some English teachers turned corporate "education experts", and a few mystery people with apparently no background in anything!
DeleteCommon Core State Standards Initiative >>>>> Download Now
Delete>>>>> Download Full
Common Core State Standards Initiative >>>>> Download LINK
>>>>> Download Now
Common Core State Standards Initiative >>>>> Download Full
>>>>> Download LINK QE
I've been teaching my third grade son about fractions recently.
ReplyDeleteAnd I guess I'm just a big ol' dummy because I showed him that a whole number such as 3 could be represented as 3/1 and that he could multiply any fraction by 1 and get the same fraction with a different denominator multiplying by 1 , where 1=n/n.
Of course, he speaks Mandarin, but I've been teaching him in English, so maybe I'll switch to fenzi and fenmu to see if it helps.
But so far he seems to understand. All it takes is some practice.
Seriously, we set the bar way too low for our kids.
BTW, he's already scoring at a 5th grade level on his math tests, so maybe I'm doing something right after all...
Gawd knows the crap they're teaching him in the school is a bunch of worthless, wordy BS.
Giving the kids examples, diagrams, pictures, etc. and practice help a lot.
All the fancy words just get in the way.
I throw something at him and if it sticks, great, if not, then we try again later.
3rd grade "progression" be damned.
I would still question if he really understands fractions and is able to answer more thought-provoking and abstract questions than the straightforward "problems" that he is undoubtedly very good at computing. There is a world of difference between being able to "multiply across" to get the right answer, and being able to show or explain or justify why when you multiply whole numbers the answer gets bigger, but with fractions the answers get smaller.
DeleteCommon Core State Standards Initiative >>>>> Download Now
ReplyDelete>>>>> Download Full
Common Core State Standards Initiative >>>>> Download LINK
>>>>> Download Now
Common Core State Standards Initiative >>>>> Download Full
>>>>> Download LINK
I read this blog very useful content thank you
ReplyDelete0.95 as a fraction